Revision history [back]

The picture is really helpful to undersand what you have really. Neglecting the corners, what you end up having is a repeatable pattern of half of a panel, an I-Beam and then another half of a panel.

The I-Beam will have a substantially lower R-value, or a higher U-value, meaning heat will tend to flow through it a lot more. This will create a pretty strong thermal bridge.

Now there are different ways you can take that into account, depending on how much work you want to do:

• The crude way: take the area-weighted U-value. $\frac{(UA)_{beam} * (UA)_{wall}}{A_{beam} + A_{wall}}
• The librarian way (useful for QA/QC too...): try to find your wall construction in a library of thermal bridges, use the listed $\psi$ value (W/m.K or BTU/h.ft.R) and calculate the resulting U-value
• The better way: calculate a proper thermal bridge using a 2D (or even 3D...) heat-transfer software such as LBNL's THERM.

Note that in the case where you have multiple layers and say one layer is bridge (example: you have concrete and I-beams in the first layer, and behind it you have continuous insulation), the crude way is actually to calculate the series and the parallel heat flow and to take the average between the two. (note to self: include reference to ASHRAE HoF, Chapter on Heat Transfer)

The picture is really helpful to undersand what you have really. Neglecting the corners, what you end up having is a repeatable pattern of half of a panel, an I-Beam and then another half of a panel.panel¹.

The I-Beam will have a substantially lower R-value, or a higher U-value, meaning heat will tend to flow through it a lot more. This will create a pretty strong thermal bridge.

Now there are different ways you can take that into account, depending on how much work you want to do:

• The crude way: take the area-weighted U-value. $\frac{(UA)_{beam} * (UA)_{wall}}{A_{beam} + A_{wall}}
• The librarian way (useful for QA/QC too...): try to find your wall construction in a library of thermal bridges, use the listed $\psi$ value (W/m.K or BTU/h.ft.R) and calculate the resulting U-value
• The better way: calculate a proper thermal bridge using a 2D (or even 3D...) heat-transfer software such as LBNL's THERM.

Note that in the case where you have multiple layers and say one layer is bridge (example: you have concrete and I-beams in the first layer, and behind it you have continuous insulation), the crude way is actually to calculate the series and the parallel heat flow and to take the average between the two. (note to self: include reference to ASHRAE HoF, Chapter on Heat Transfer)

The picture is really helpful to undersand what you have really. Neglecting the corners, what you end up having is a repeatable pattern of half of a panel, an I-Beam and then another half of a panel¹.

The I-Beam will have a substantially lower R-value, or a higher U-value, meaning heat will tend to flow through it a lot more. This will create a pretty strong thermal bridge.

Now there are different ways you can take that into account, depending on how much work you want to do:

• The crude way: take the area-weighted U-value. $\frac{(UA)_{beam} * (UA)_{wall}}{A_{beam} + A_{wall}}
• The librarian way (useful for QA/QC too...): try to find your wall construction in a library of effective wall R/U-value, such as in ASHRAE litterature (wood/metal studs walls are covered for example). If you can't, search in a library of thermal bridges, use the listed $\psi$ value (W/m.K or BTU/h.ft.R) and calculate the resulting derated U-value
• The better way: calculate a proper thermal bridge using a 2D (or even 3D...) heat-transfer software such as LBNL's THERM.

Note that in the case where you have multiple layers and say one layer is bridge bridged (example: you have concrete and I-beams in the first layer, and behind it you have continuous insulation), the crude way is actually to calculate the series and the parallel heat flow and to take the average between the two. (note to self: include reference to slightly different depending on how different the conductivities of dissimilar materials are:

• The parallel- path method is used when the thermal conductivity of the dissimilar materials in the layer are rather close in value (within the same order of magnitude), as with wood-frame walls
• The isothermal-planes method is appropriate for materials with conductivities moderately different from those of adjacent materials (e.g., masonry).
• The zone method and the modified zone method are appropriate for materials with a very high difference in conductivity (two orders of magnitude or more), such as with assemblies containing metal.

See this illustration taken from Chapter 27 of the HoF:

References:

• ASHRAE HoF, Handbook of Fundamentals, Chapter 4 "Heat Transfer"
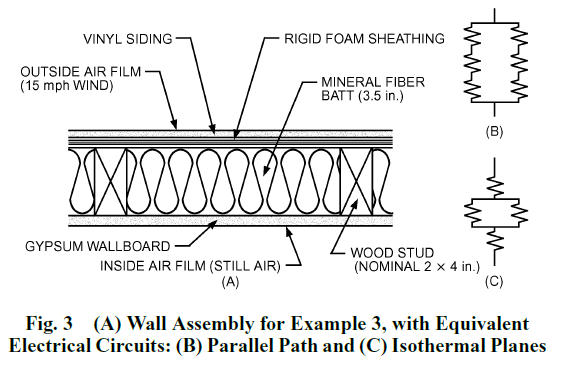
• Chapter 27 "HEAT, AIR , AND MOISTURE CONTROL IN BUILDING ASSEMBLIES—EXAMPLES"

My two cents if you have to use some complicated manual calculations such as for the zone method: you end up being faster and more accurate using THERM once you get the gist of it, and that includes how to draw properly in THERM and how to set your boundary conditions properly and on Heat Transfer)which surface to define the R-value calculation. There's a learning curve, but there's also pretty good documentation out there (thanks to standards such as Passivhaus who have got people interested in calculating bridges properly, and it's a worthy investment IMHO.

¹Note that it actually reduces to half a panel and half an I-beam due to symmetry, but it's harder to grasp / visualize if you use THERM or another heat transfer software.