How does CondFD deal with no-mass materials?
I'm assessing the performance of a DOE office building using different envelope materials. I'm using phase change materials and comparing the EUI/TEDI with the original envelope (thermal insulation). The thing is that this insulation, in the original model, is represented by a thermal resistance only, i.e., a Material:NoMass class, which doesn't require other properties such as density or specific heat, other than the R-value and absorptance values (thermal, solar and visible).
Since CondFD uses a dynamic spatial discretization depending on the material's physical and thermal properties, how does the algorithm discretize a no-mass material? What information will it use?
I don't get any errors simulating the original thermal insulation, though. In fact, the results seem to be really coherent, but I need to understand the software's procedure.
Reading the engineering reference, the CTF algorithm has a solution for the no-mass materials:
For “no mass” layers, the density (rho) and the specific heat (cp) variables will be assigned zero values. In addition, the thickness (dx) will be equated with the user-defined R-Value and conductivity (rk) will be assigned a value of unity. In addition, the number of nodes for the “no mass” layer will be set to 1. This handles resistive layers correctly without resorting to assigning the properties of air to the “no mass” layer.
Thinking upon the fully-implicit scheme used in the CondFD to solve the heat diffusion equation (the scheme I'm using), this approach would eliminate the energy storage term, the transient term.
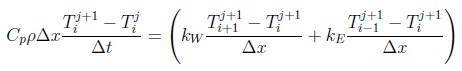
This would leave us with temperature terms with respect to iteration j+1, which doesn't make much sense. Does CondFD correct this?
After all, this would transform a transient problem into a steady state problem within the control volume of the no-mass material, with time-dependent boundary conditions, while the other wall layers still have transient behaviors





