Motor In Airstream fraction is acting weird

asked 7 years ago

Kingo

351 ●1 ●6

updated 7 years ago

__AmirRoth__

4446 ●5 ●17 http://bleedinggreenna...

Found a weird thing with the Mortor in Airstream fraction that is input for Fans in OpenStudio. From what i understand, when the value is 0, it should not provide any heat to the airstream. But that is not the case, which made me wonder if something is wrong when it translated into the idf file.

I also noticed that there is a small difference between setting it to 1 or 0. But it still gain some heat from the fan, so is that cause by something else? The two examples are shown in the figures below:

Motor In Airstream Fraction = 0.0 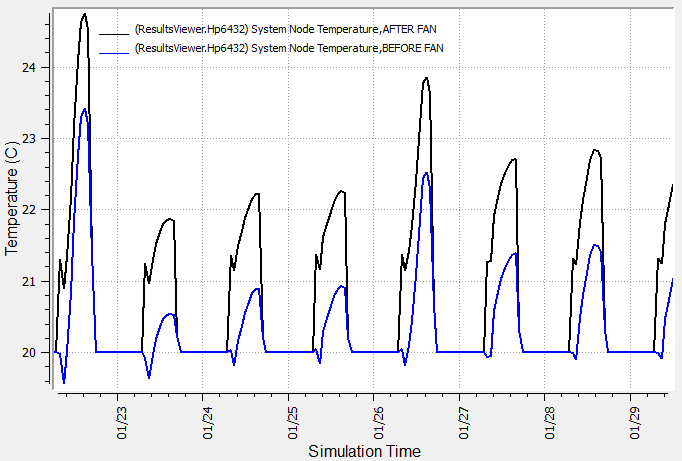image description

Motor In Airstream Fraction = 1.0 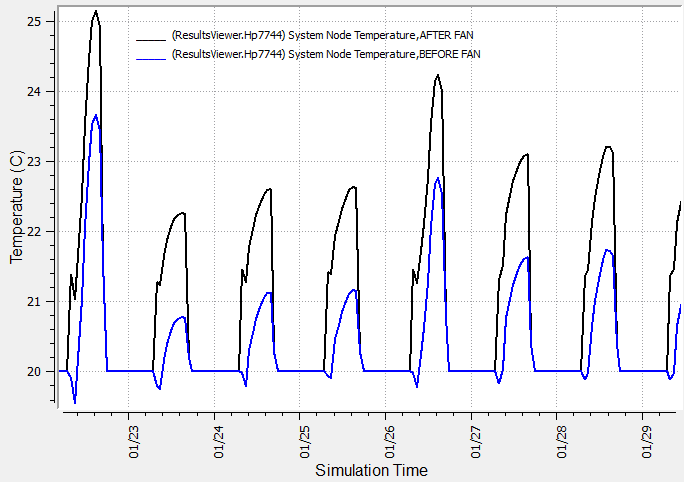image description

The HVAC system used: 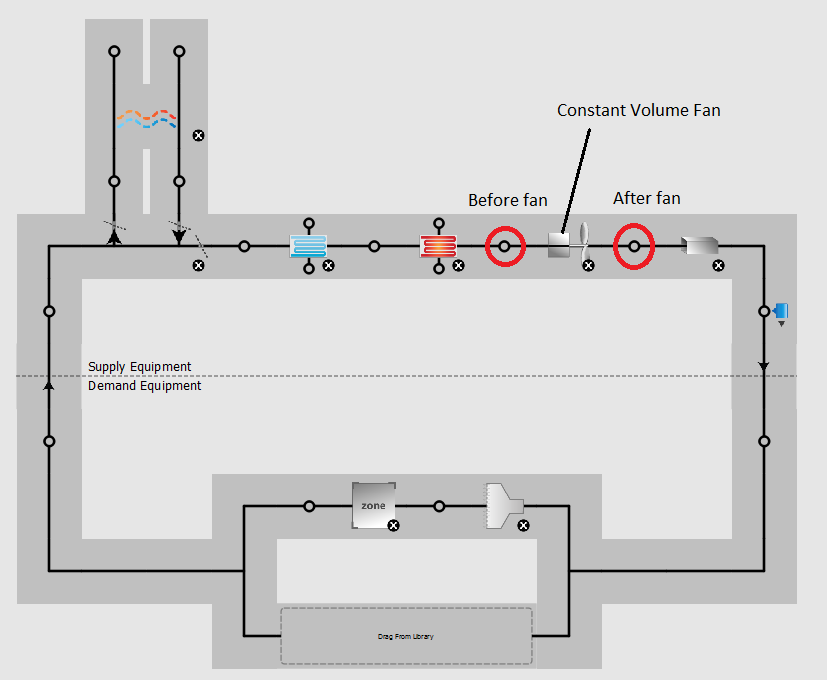image description

Hope someone can enlighten me :)

add a comment

2 Answers

Sort by » oldest newest most voted

answered 7 years ago

Adam Hilton

3475 ●1 ●15

updated 7 years ago

From the engineering reference...

$Q_{toair} = H_{fan} + (H_{motor} - H_{fan}) * f_{motortoair}$

While not discussed in the fan section, I assume it's the same logic as pumps. Any shaft power is eventually realized as heat to the fluid due to friction losses. I'm not actually a fan of that because in the real world, you're not controlling to those losses because that heat would be added after any kind of discharge air controller.

link

Comments

Are you sure you didn't mean to have $Q_{toair} = H_{fan} + (H_{tot} - H_{fan}) * f_{motortoair}$ ? I could be misinterpreting your notation but the way you have it written if $f_{motortoair}=1$ you would have $Q_{toair} = H_{motor}$ but if the motor is totally in the air stream I believe you should have $Q_{toair} = H_{tot}$ .

Jeremy ( 7 years ago )

$H_{motor} = H_{tot}$ $H_{motor} = H_{fan} / \eta_{belt} / \eta_{motor}$

Adam Hilton ( 7 years ago )

add a comment

answered 7 years ago

kpp
219 ●1 ●7

updated 7 years ago

This is interesting. As Adam mentioned, I checked the equations in 17.4 Air System Fans. From the equations (17.131 to 17.136), even if f_motortoair is 0, it does not imply the Q_toAir variable is 0, therefore, the enthalpy of air at the outlet is not equal to enthalpy at the inlet. (check the derived equations in image)

h_out > h_in

The psychrometric function (eq. 17.136) calculates fan outlet drybulb temperature higher than the inlet fan air temperature. Therefore even if f_motortoair = 0, there is addition of heat and T_out > T_in.

image description

link

add a comment

Your Answer

Please start posting anonymously - your entry will be published after you log in or create a new account.

Add Answer

Motor In Airstream fraction is acting weird

2 Answers

Comments

Your Answer

Training Workshops

Careers

Question Tools

Stats

Motor In Airstream fraction is acting weird savecancel

2 Answers

Comments

Your Answer

Training Workshops

Careers

Question Tools

Stats

Motor In Airstream fraction is acting weird