First time here? Check out the Help page!
 | 1 | initial version |
I suggest you first read the Input/Output reference guide for the People object to get a better idea of how it's defined, and what parameter affect the heat generation. You'll want to play close attention to the Sensible Heat Fraction field, which defaults to autocalculate.
Then once you have understood how the People object is characterized, you can read the engineering reference which happens to have a short (that's nice!) section that answers your question called Heat Gain from People
You'll learn that the the Sensible gain is derived from a polynomial function of Temperature and Metabolic rate, and get a representation of the Sensible Heat Gain as a function of metabolic rate for different temperatures.
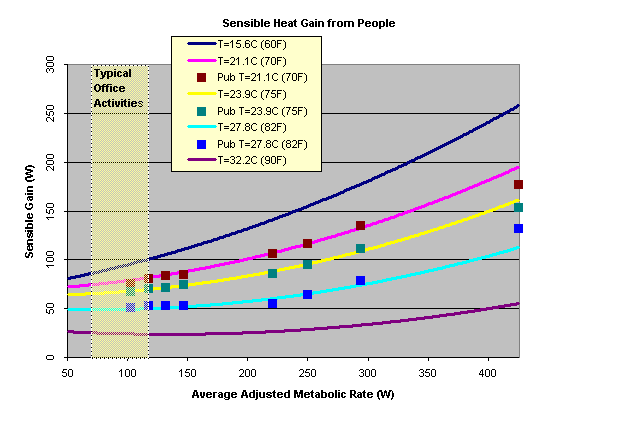
Given that Latent Gain = Metabolic Rate - Sensible Gain, and that the latent gain is the one that "adds water" like you said, it's easy to see that an increase in temperature will produce more latent gain. That's why you see more humidity in the summer, because the indoor space temperature is higher than the winter. It's also quite logical, since you tend to sweat more when its hotter.
In case you have trouble reading the above graph, I went ahead and created a clearer one, where I fixed the metabolic rate to 120W (typical office activity), then used the polynomial equation to create the split between sensible and latent as a function of temperature.
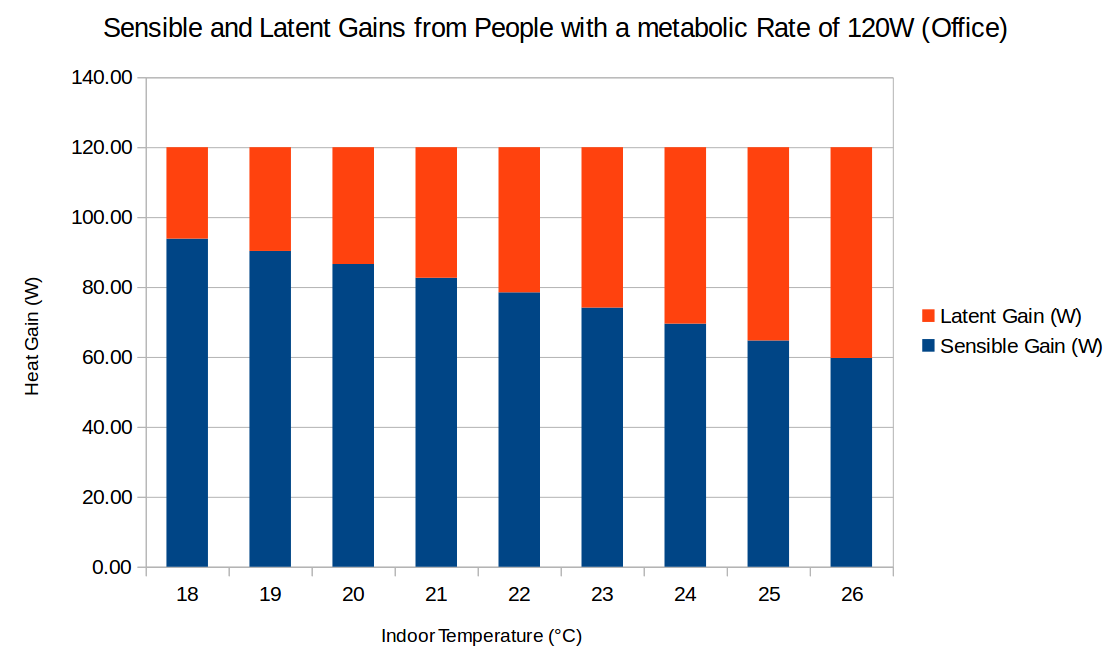
 | 2 | No.2 Revision |
I suggest you first read the Input/Output reference guide for the People object to get a better idea of how it's defined, and what parameter affect the heat generation. You'll want to play close attention to the Sensible Heat Fraction field, which defaults to autocalculate.
Then once you have understood how the People object is characterized, you can read the engineering reference which happens to have a short (that's nice!) section that answers your question called Heat Gain from People
You'll learn that the the Sensible gain is derived from a polynomial function of Temperature and Metabolic rate, and get a representation of the Sensible Heat Gain as a function of metabolic rate for different temperatures.

Given that Latent Gain = Metabolic Rate - Sensible Gain, and that the latent gain is the one that "adds water" like you said, it's easy to see that an increase in temperature will produce more latent gain. That's why you see more humidity in the summer, because the indoor space temperature is higher than the winter. It's also quite logical, since you tend to sweat more when its hotter.
In case you have trouble reading the above graph, I went ahead and created a clearer one, where I fixed the metabolic rate to 120W (typical office activity), then used the polynomial equation to create the split between sensible and latent as a function of temperature.

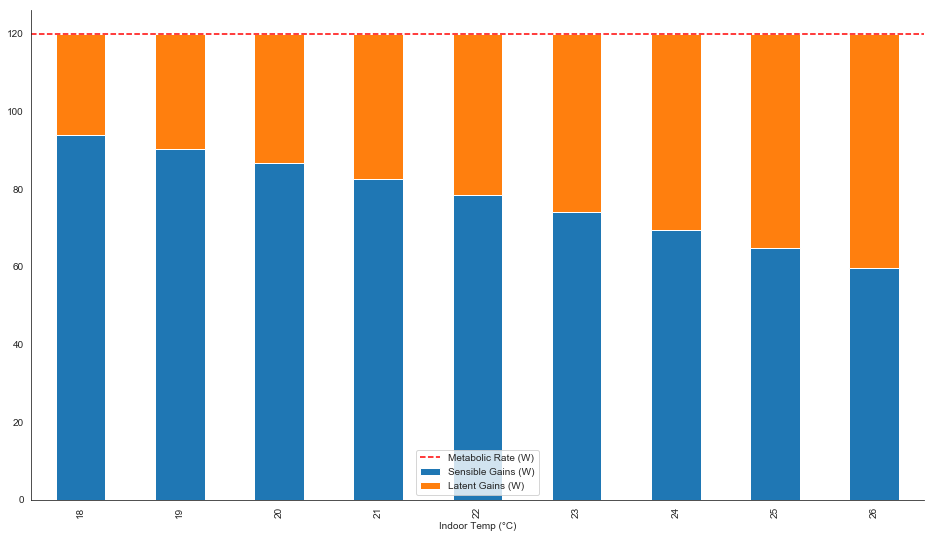
 | 3 | No.3 Revision |
I suggest you first read the Input/Output reference guide for the People object to get a better idea of how it's defined, and what parameter affect the heat generation. You'll want to play close attention to the Sensible Heat Fraction field, which defaults to autocalculate.
Then once you have understood how the People object is characterized, you can read the engineering reference which happens to have a short (that's nice!) section that answers your question called Heat Gain from People
You'll learn that the the Sensible gain is derived from a polynomial function of Temperature and Metabolic rate, and get a representation of the Sensible Heat Gain as a function of metabolic rate for different temperatures.

Given that Latent Gain = Metabolic Rate - Sensible Gain, and that the latent gain is the one that "adds water" like you said, it's easy to see that an increase in temperature will produce more latent gain. That's why you see more humidity in the summer, because the indoor space temperature is higher than the winter. It's also quite logical, since you tend to sweat more when its hotter.
In case you have trouble reading the above graph, I went ahead and created a clearer one, where I fixed the metabolic rate to 120W (typical office activity), then used the polynomial equation to create the split between sensible and latent as a function of temperature.

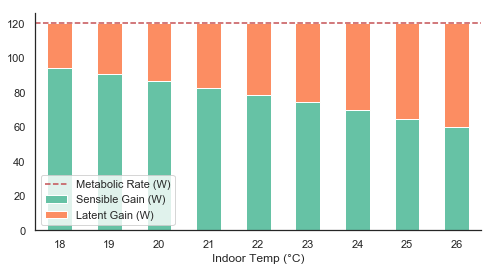
 | 4 | No.4 Revision |
I suggest you first read the Input/Output reference guide for the People object to get a better idea of how it's defined, and what parameter affect the heat generation. You'll want to play close attention to the Sensible Heat Fraction field, which defaults to autocalculate.
Then once you have understood how the People object is characterized, you can read the engineering reference which happens to have a short (that's nice!) section that answers your question called Heat Gain from People
You'll learn that the the Sensible gain is derived from a polynomial function of Temperature and Metabolic rate, and get a representation of the Sensible Heat Gain as a function of metabolic rate for different temperatures.

Given that Latent Gain = Metabolic Rate - Sensible Gain, and that the latent gain is the one that "adds water" like you said, it's easy to see that an increase in temperature will produce more latent gain. That's why you see more humidity in the summer, because the indoor space temperature is higher than the winter. It's also quite logical, since you tend to sweat more when its hotter.
In case you have trouble reading the above graph, I went ahead and created a clearer one, where I fixed the metabolic rate to 120W (typical office activity), then used the polynomial equation to create the split between sensible and latent as a function of temperature.

Edit: Unrelated to your original question, but I find it interesting anyways and thought people might too: I noticed something on the curve from the engineering reference: at low metabolic rates, the sensible gain is above the metabolic rate (=total gain), which is physically problematic (sic!).
So I plotted a heatmap to check that, putting in bright red the region where the latent gain ends up negative as a result.
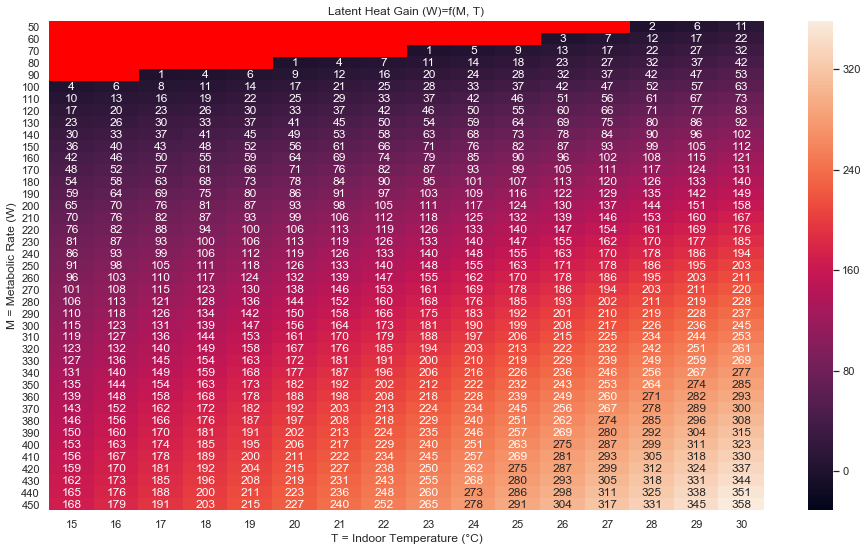
FYI, reading the source code around here what happens in this case is that the sensible gain is set to the metabolic rate, and the latent gain ends up 0 as a result.
 | 5 | No.5 Revision |
I suggest you first read the Input/Output reference guide for the People object to get a better idea of how it's defined, and what parameter affect the heat generation. You'll want to play close attention to the Sensible Heat Fraction field, which defaults to autocalculate.
Then once you have understood how the People object is characterized, you can read the engineering reference which happens to have a short (that's nice!) section that answers your question called Heat Gain from People
You'll learn that the the Sensible gain is derived from a polynomial function of Temperature and Metabolic rate, and get a representation of the Sensible Heat Gain as a function of metabolic rate for different temperatures.

Given that Latent Gain = Metabolic Rate - Sensible Gain, and that the latent gain is the one that "adds water" like you said, it's easy to see that an increase in temperature will produce more latent gain. That's why you see more humidity in the summer, because the indoor space temperature is higher than the winter. It's also quite logical, since you tend to sweat more when its hotter.
In case you have trouble reading the above graph, I went ahead and created a clearer one, where I fixed the metabolic rate to 120W (typical office activity), then used the polynomial equation to create the split between sensible and latent as a function of temperature.

Edit: Unrelated to your original question, but I find it interesting anyways and thought people might too: I noticed something on the curve from the engineering reference: at low metabolic rates, the sensible gain is above the metabolic rate (=total gain), which is physically problematic (sic!).
So I plotted a heatmap to check that, putting in bright red the region where the latent gain ends up negative as a result.

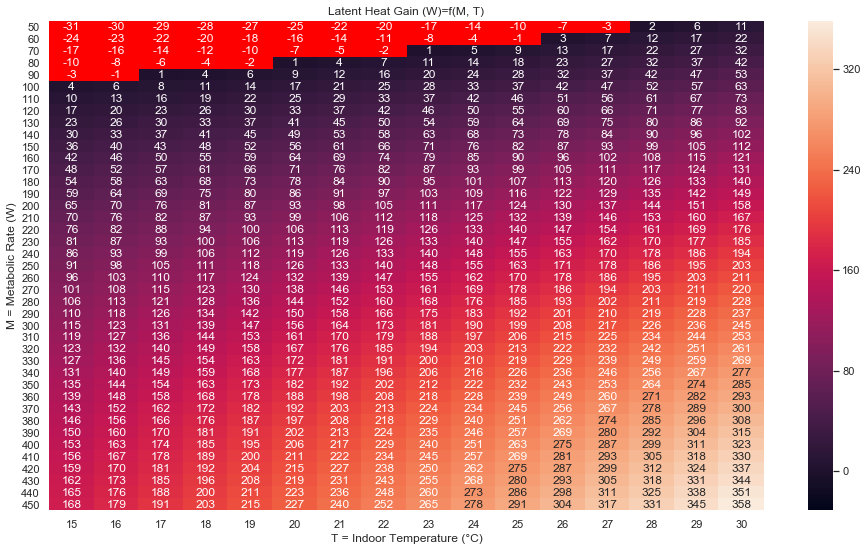
FYI, reading the source code around here what happens in this case is that the sensible gain is set to the metabolic rate, and the latent gain ends up 0 as a result.
 | 6 | No.6 Revision |
I suggest you first read the Input/Output reference guide for the People object to get a better idea of how it's defined, and what parameter affect the heat generation. You'll want to play close attention to the Sensible Heat Fraction field, which defaults to autocalculate.
Then once you have understood how the People object is characterized, you can read the engineering reference which happens to have a short (that's nice!) section that answers your question called Heat Gain from People
You'll learn that the the Sensible gain is derived from a polynomial function of Temperature and Metabolic rate, and get a representation of the Sensible Heat Gain as a function of metabolic rate for different temperatures.

Given that Latent $Latent Gain = Metabolic Rate - Sensible Gain, Gain$, and that the latent gain is the one that "adds water" like you said, it's easy to see that an increase in temperature will produce more latent gain. That's why you see more humidity in the summer, because the indoor space temperature is higher than the winter. It's also quite logical, since you tend to sweat more when its hotter.
In case you have trouble reading the above graph, I went ahead and created a clearer one, where I fixed the metabolic rate to 120W (typical office activity), then used the polynomial equation to create the split between sensible and latent as a function of temperature.

Edit: Unrelated to your original question, but I find it interesting anyways and thought people might too: I noticed something on the curve from the engineering reference: at low metabolic rates, the sensible gain is above the metabolic rate (=total gain), which is physically problematic (sic!).
So I plotted a heatmap to check that, putting in bright red the region where the latent gain ends up negative as a result.

FYI, reading the source code around here what happens in this case is that the sensible gain is set to the metabolic rate, and the latent gain ends up 0 as a result.
